李宏毅ml note

Intro

Traning

Function

使用 model: $y = b+wx_{1}$
其中，$w$ 表示 weight，$b$ 表示 bias

Loss function

表示： $L(b,w)$

Optimization

一般性方法： 梯度下降法（gradient descent）

• 选择起始点 $w_0$
• 计算梯度 $\eta\frac{\partial L}{\partial w}|_{w = w^0}$ ($\eta$ 表示学习率 learning rate)
• 更新 w: $w_1 \leftarrow w_{0 }-\eta\frac{\partial L}{\partial w}|_{w = w^0}$
• b 作同样操作使 L 最小

More sophisticated models

多个 model 叠加

线性叠加

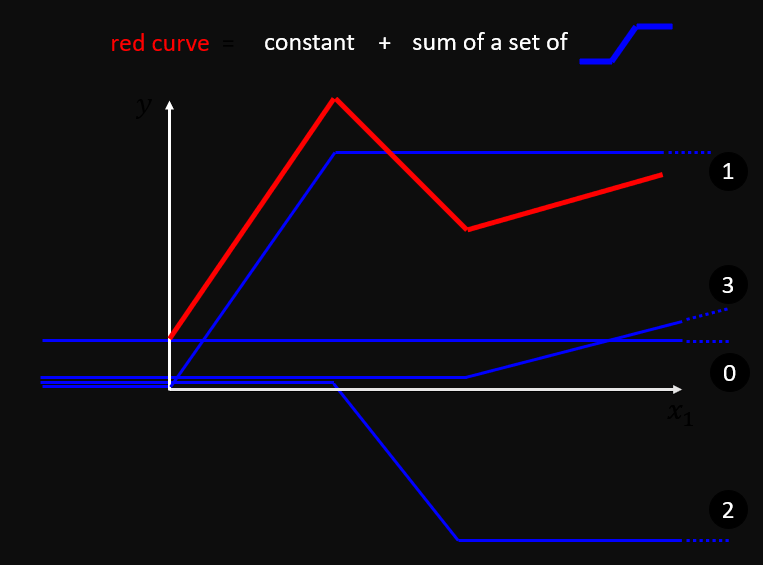
使用多个线性 model 叠加即可得到更为复杂的函数拟合曲线

Sigmoid func

$$\begin{align} y &= c\frac{1}{1+e^{ -(b+wx_{1}) } }\\&=csigmoid(b+wx_{1}) \end{align}$$

使用 sigmoid 方程代替线性叠加可以得到所有的函数拟合，最终得到

$$y = b+\sum_{i} c_{i} sigmoid\left( b_{i}+\sum_{j}w_{ij}x_{j} \right)$$

即：

$$y = b+c^{T} \sigma(b+Wx)$$

j: no. of features
i: no. of sigmoid

ReLu func

$$y = \max\{0,x\}$$

Loss

$$L = \frac{1}{N} \sum_{n} e_{n}$$

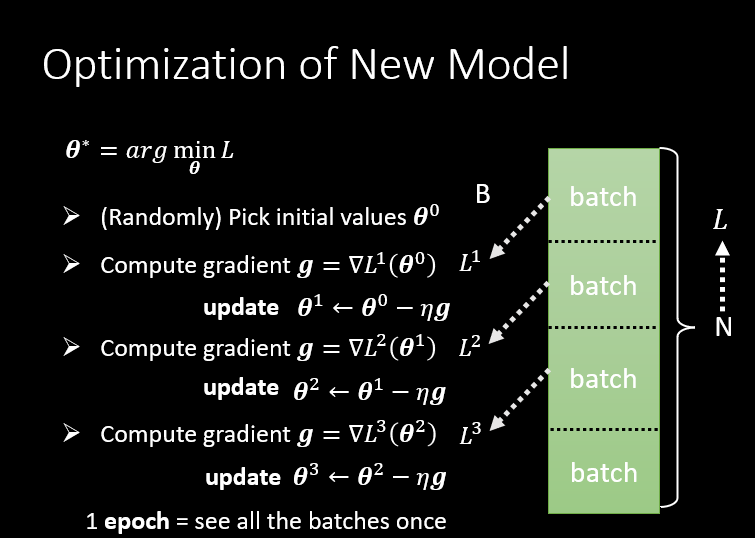
Optimization

$\theta^* = \arg \min_{\theta}L$
梯度矩阵

$$\mathbf{g} = \nabla L(\theta^0)$$

$$\mathbf{\theta^1} \leftarrow \mathbf{ \theta^{0}} - \eta\mathbf{ g}$$

在实际训练中，通常使用 batch 将原始数据集分解成不同的 batch 单独计算。