CSP

概述

组成

  • A special subset of search problems.
  • State is defined by variables XiX_i with values from a
    domain DD (sometimes D depends on i).
  • Goal test is a set of constraints specifying allowable
    combinations of values for subsets of variables

分类

  • Binary CSP: each constraint relates (at most) two
    variables.
  • Binary constraint graph: nodes are variables, arcs
    show constraints.
  • General-purpose CSP algorithms use the graph
    structure to speed up search.

变量

  • 离散变量

    • 有限域

    • 无限域

  • 连续变量

解决问题

约束满足问题传统上是使用一种称为backtracking search回溯搜索的搜索算法来解决的。回溯搜索是深度优先搜索的一种优化，专门用于约束满足问题，其改进来自两个主要原则：

  1. Fix an ordering for variables, and select values for variables in this order. Because assignments are commutative
  2. When selecting values for a variable, only select values that don’t conflict with any previously assigned values. If no such values exist, backtrack and return to the previous variable, changing its value.

algorithm

Filtering

Keep track of domains for unassigned variables and cross off bad options.

A naïve method

Forward checking: Cross off values that violate a constraint when added to the existing assignment

Arc consistency

An arc X → Y is consistent iff:

For every x in the tail there is some y in the head which could be assigned without violating a constraint.

Remember:Delete from the tail!

Important: If X loses a value, neighbors of X need to be rechecked!

示意图

algorithm：

算法2

K-Consistency

For each k nodes, any consistent assignment to k-1 can
be extended to the kth node.

Strong k-consistency: also k-1, k-2, … 1 consistent

Ordering

  • Minimum Remaining Values means Choose the variable with the fewest legal left values in its domain.在选择下一个要分配的变量时，使用 MRV 策略会选择未分配的变量中有效剩余值最少的变量（最受约束的变量）。这是直观的，因为最受约束的变量最有可能用尽可能的值，并且如果未分配则导致回溯，因此最好尽早为其分配值。
  • Least Constraining Value means Given a choice of variable, choose the least constraining value.在选择下一个要分配的值时，一个好的策略是选择从剩余未分配值的域中修剪最少值的值。值得注意的是，这需要额外的计算（例如，重新运行弧一致性/前向检查或每个值的其他过滤方法以找到 LCV），但仍可以根据使用情况提高速度。

Structure

In particular, if we’re trying to solve a tree-structured CSP (one that has no loops in its constraint graph), we can reduce the runtime for finding a solution from O(dN)O(d^N) all the way to O(nd2)O(nd^2)​, linear in the number of variables.

  • pick an arbitrary node as the root.
  • Convert all undirected edges in the tree to directed edges that point away from the root.简单来说，这只是意味着对图的节点进行排序，使所有边都指向右侧。
  • Perform a backwards pass of arc consistency.
  • perform a forward assignment.
  • This can be extended to CSPs that are reasonably close to being tree-structured with cutset conditioning.一旦找到最小的割集，我们就分配其中的所有变量，并修剪所有相邻节点的域。

Local search methods typically work with “complete” states.

  • Local search: improve a single option until you can’t make it better (no fringe!)
  • Hill Climbing: Start wherever and move to the best neighboring state. If no neighbors better than current, quit.

Adversarial (Game)

What is game

  • Many agents.
  • Want algorithms for calculating a strategy which recommends a move from each state.
    我们一般处理的是两个Agent 之间的确定性零和博弈，即: 两个Agent 之间是竞争关系；Agent 的采取特定 Action 后对于环境的影响是确定的(Deterministic).

Types of game

Deterministic games

Formalizations:

  • States: S (start at s0)
  • Players: P = {1…N} (usually take turns)
  • Actions: A (may depend on player / state)
  • Transition Function: S x A ->S
  • Terminal Test: S ® {t, f}
  • Terminal Utilities: S x P -> R

Zero-sum games

  • Agents have opposite utilities
  • Lets us think of a single value that one maximizes and the other minimizes
  • Adversarial, pure competition

General games

  • Agents have independent utilities (values on outcomes)
  • Cooperation, indifference, competition, and more are all possible

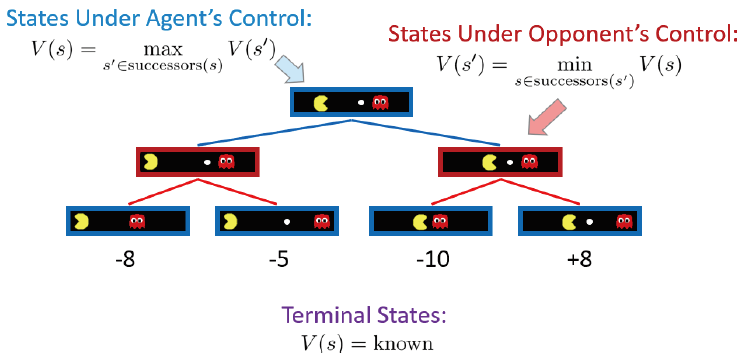
Minimax tree

Value of a state means the best achivable outcome from that state, and specifically for a Non-terminal state, $$MAX:V(s) = \max_{s’ \in children(s) }V(s’) $$$$MIN:V(s) = \min_{s’ \in children(s) }V(s’) $$

  • A state-space search tree
  • Players alternate turns
  • Compute each node’s minimax value: the best achievable utility against a rational (optimal) adversary
    minimax tree

How to bulid

伪代码如下所示：

1
2
3
4
5
6
7
def value(state):
    if the state is a terminal state:
        return the utility
    if the nextAgent is MAX: 
        return max_value(state)
    if the nextAgent is MIN: 
        return min_value(state)

Max 和 Min 计算如下：

1
2
3
4
5
def max_value(state):
    initialize = -infty
    for each successor of state:
	    v = max(v,min_value(successor))
    return v 
1
2
3
4
5
def min_value(state):
    initialize = +infty
    for each successor of state:
        v = min(v,min_value(successor))
    return v

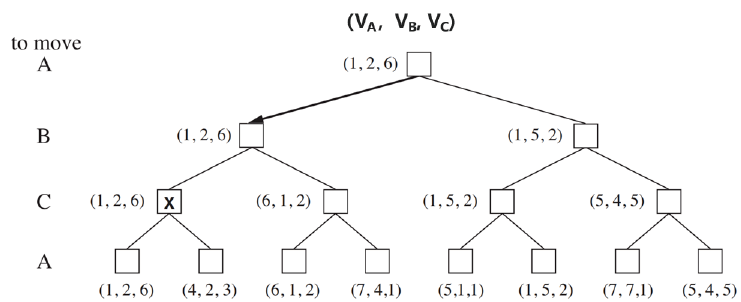
拓展:Multi-Agent Utilities

以上流程可以拓展到多个 Player 的博弈过程，如图 4 所示，每次进行决策时都以到达对己方最大收益的 Terminal State 为依据即可。
more

Efficiency

在 Minimax Tree 中，由于中间非终止状态的收益需要通过叶子节点的
终止状态回溯得到。因此，可以通过类似于 DFS 的过程得到整棵 Minimax
Tree 中每个状态的收益，从而为 MAX Player 和 MIN Player 的 Action 决
策提供依据。根据 DFS 的性质，标准的 Minimax Tree 满足：

  • Just like DFS
  • Time comlexity: O(bm)O(b^m)
  • Space complexity: O(bm)O(bm)

α−β\alpha - \beta Pruning

α\alpha: MAX’s best option on path to root
β\beta: MIN’s best option on path to root
Max 和 Min 计算如下：

1
2
3
4
5
6
7
8
def max_value(state,alpha,beta):
    initialize = -infty
    for each successor of state:
	    v = max(v,value(successor,alpha,beta))
	    if(v>=beta):
	        return v
	    alpha = max(alpha,v)
    return v 
1
2
3
4
5
def min_value(state):
    initialize = +infty
    for each successor of state:
        v = min(v,min_value(successor))
    return v

“Alpha-Beta”剪枝算法效率高度依赖于节点访问顺序。

Resource Limit

In realistic games, cannot search to leaves.
Solution: Depth-limited search

  • Instead, search only to a limited depth in the tree
  • Replace terminal utilities with an evaluation function for non-terminal positions
    设定最大搜索深度 D，对于搜索树的孩子节点，基于 Evaluation Function 估计其收益，随后根据 Minimax Tree 的估计流程，自下而上地估计所有状态的收益，从而进行决策。

Expectimax

About

Why wouldn’t we know what the result of an action will be?

  • Explicit randomness: rolling dice
  • Unpredictable opponents: the ghosts respond randomly
  • Unpredictable humans: humans are not perfect
  • Actions can fail: when moving a robot, wheels might slip
    Values should now reflect average-case (expectimax) outcomes, not worst-case (minimax) outcomes.
    Expectimax search: compute the average score under optimal play
  • Max nodes as in minimax search
  • Chance nodes are like min nodes but the outcome is uncertain
  • Calculate their expected utilities
  • I.e. take weighted average (expectation) of children
    伪代码如下：
1
2
3
4
5
6
def exp_value(state):
initialize v = 0
for each successor of state:
    p = probability(successor)
v += p * value(successor)
    return v

这里的核心问题在于如何估计 probability (successor)，也即 π(ai∣s)\pi (a_{i}|s) 这一过程将在强化学习章节继续讲述。

utilities

Utilities are functions from outcomes(states of the world) to real numbersthat describe an agent’s preferences.

where they come from

  • In a game, may be simple (+1/-1)
  • Utilities summarize the agent’s goals
  • Theorem: any “rational” preferences can be summarized as a utility function

preferences

An agent must have prefernces among prizes:A,B,etc.

Preference:A≻BA \succ B

Indifference:A∼BA \sim B

The axioms(公理) of rationality

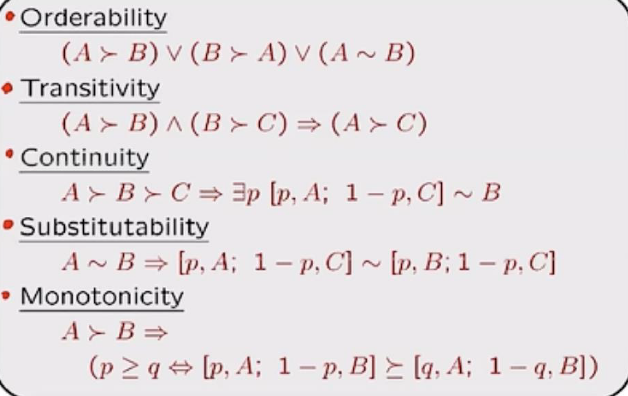
axioms

MCTS 通过不断模拟游戏的可能走法（随机采样），并逐步构建一棵搜索树，最终选择最优动作。它不需要完整枚举所有可能，仅通过模拟获得近似最优解。

  • Evaluation by rollouts – play multiple games to termination from a state s (using a simple, fast rollout policy) and count wins and losses
  • Selective search – explore parts of the tree that will help improve the decision at the root, regardless of depth