Intro

Search: Formulation and Solution (s)

Agent categories

Rational agent

Reflex agent

Planning agent

  • Have the model of how the world evolves.
  • Optimal and replannning.

Formulation

Basic Elements of Search Problem

  • State Space
    • world state
    • search state
  • Successor Function
  • Start state (to start the search) and goal test (to terminate the search)
  • Solution

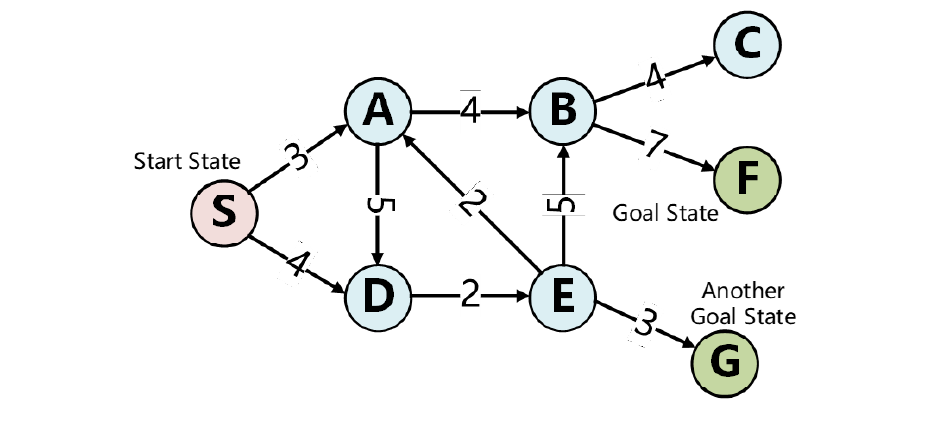
Search graph

A mathematical formulation of Search Problem: G={V, E}

  • Nodes V: States IN State Space
  • Edges/Arcs E: Successor Functions from states to successors;
  • We still have a start state and goal test
  • Solution: Path on the state graph from the start state to pass the goal test.
  • Issues:
    • In a state space graph, each state occurs only once!
    • We can rarely build this full graph in memory
      search graph

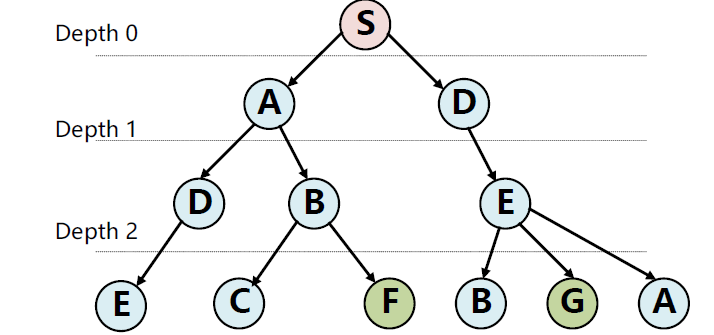
Search tree

To unravel a graph into a tree, choose a root node and trace every path from that node until you reach a leaf node or a node already in that path.
根节点为 Start State，根据 Successor Function 按需构建树，树的构建过程称为Expansion。基于 Search Tree 的搜索过程即是从根节点开始，不断探访新的 State，直到找到满足 Goal Test 的 State，或者找不到（即无解）。一个节点可能在 Search Tree 中出现多次，但在统一 path 中只出现一次。
search tree

  • Partial Plan: From S to current state
  • Expansion: Add a new state to partial plan
  • Fringe: A queue of partial plans under consideration
  • Exploration Strategy: Choose partial plan in fringe for Expansion.
    如果符合 Goal Test 则找到了解；如果直到 Fringe 为空并且无法进行新的 State 扩展时，仍然未找到解，则该搜索问题无解。

Solutions

Uninformed Search Strategies（非启发式搜索）

Evaluations

Strategies are evaluated along the following dimensions

  • Completeness: Find a solution or not?
  • Time Complexity: Number of expansion.
  • Space Complexity: Max number of nodes in memory.
  • Measured by:
    • b: max branching factor of the search tree;
    • d: depth of the least-cost solution;
    • m: max depth of the state space;
  • Optimality: Find the least-cost solution or not?

DFS

DFS 算法需要注意移除 Path 中相同的 State，防止陷入无限循环。

  • Completeness: Yes；
  • Optimality: No ；
  • Time Complexity: O (bmb^m)；
  • Space Complexity: O (bm)；

code diaplay:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
def depthFirstSearch(problem):
    "*** YOUR CODE HERE ***"

    path = util.Path([problem.getStartState()], [], 0)
    if problem.isGoalState(problem.getStartState()):
        return []

    fringe = util.Stack()
    fringe.push(path)

    while not fringe.isEmpty():
        current_path = fringe.pop()
        current_loc = current_path.locations[-1]
        if problem.isGoalState(current_loc):
            return current_path.actions
        else:
            successors = problem.getSuccessors(current_loc)
            if bool(successors):
                for successor in successors:
                    next_loc = successor[0]
                    next_action = successor[1]
                    next_cost = successor[2]
                    if next_loc not in current_path.locations:
                        locations = current_path.locations[:]
                        locations.append(next_loc)
                        all_actions = current_path.actions[:]
                        all_actions.append(next_action)
                        next_cost = current_path.cost + next_cost
                        path = util.Path(locations, all_actions, next_cost)
                        fringe.push(path)

    return []

BFS

Fringe 中 Partial Solution 的 Path 长度较短的出队优先级较高

  • Completeness: Yes；
  • Optimality: Yes （仅当状态间转移 Cost=1 时成立）；
  • Time Complexity: O (bdb^d)；
  • Space Complexity: O (bdb^d​)；

code display:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
def breadthFirstSearch(problem):
    """Search the shallowest nodes in the search tree first."""
    "*** YOUR CODE HERE ***"
    path = util.Path([problem.getStartState()], [], 0)
    if problem.isGoalState(problem.getStartState()):
        return []

    fringe = util.Queue()
    fringe.push(path)

    while not fringe.isEmpty():
        current_path = fringe.pop()
        current_loc = current_path.locations[-1]
        if problem.isGoalState(current_loc):
            return current_path.actions
        else:
            successors = problem.getSuccessors(current_loc)
            if bool(successors):
                for successor in successors:
                    next_loc = successor[0]
                    next_action = successor[1]
                    next_cost = successor[2]
                    if next_loc not in current_path.locations:
                        locations = current_path.locations[:]
                        locations.append(next_loc)
                        all_actions = current_path.actions[:]
                        all_actions.append(next_action)
                        next_cost = current_path.cost + next_cost
                        path = util.Path(locations, all_actions, next_cost)
                        fringe.push(path)

    return []

UCS (Uniform-Cost Search)：代价一致搜索

Always expand the least-cost unexpanded first
Fringe Implementation: 队列中元素的优先级取决于从 Start State 到当前 State 累积 cost 之和

  • Completeness: Yes
  • Optimality: Yes
  • Time Complexity: O (b1+⌊C∗+ϵ⌋b^{1+\lfloor C^*+\epsilon \rfloor})
  • Space Complexity: O (b1+⌊C∗+ϵ⌋b^{1+\lfloor C^*+\epsilon \rfloor}​)

code diaplay:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
def uniformCostSearch(problem):
    """Search the node of least total cost first."""
    "*** YOUR CODE HERE ***"
    path = util.Path([problem.getStartState()], [], 0)
    if problem.isGoalState(problem.getStartState()):
        return []

    fringe = util.PriorityQueue()
    fringe.push(path,path.cost)

    while not fringe.isEmpty():
        current_path = fringe.pop()
        current_loc = current_path.locations[-1]
        if problem.isGoalState(current_loc):
            return current_path.actions
        else:
            successors = problem.getSuccessors(current_loc)
            if bool(successors):
                for successor in successors:
                    next_loc = successor[0]
                    next_action = successor[1]
                    next_cost = successor[2]
                    if next_loc not in current_path.locations:
                        locations = current_path.locations[:]
                        locations.append(next_loc)
                        all_actions = current_path.actions[:]
                        all_actions.append(next_action)
                        next_cost = current_path.cost + next_cost
                        path = util.Path(locations, all_actions, next_cost)
                        fringe.push(path,path.cost)

    return []

Depth-Limited Search (DLS)

Early stop with limited depth
如果当前的 Partial Solution 的 Path 长度（深度）超过了设定阈值 d，则无法拓展新的 State。
假设当前搜索问题在 l层可以找到最优解，那么对于最大搜索深度为 l 的 DLS 算法:

  • 时间复杂度为 O (bl(b^l)
  • 空间复杂度为 O (blbl)
    否则，会增加一层继续进行 DLS

Iterative Deepening Search (IDS)

如果其状态空间大小为 m，则从 1 开始，逐步增加 DLS的最大搜索深度，直到 m，如果在这过程中找到解，则停止搜索。其基本过程是 BFS 和 DFS 的结合，相比于 DFS，避免了过度陷入较深的层；相比于 BFS，避免了从第一层到当前层每一个节点的拓展。

  • Completeness: Yes, we need to avoid duplication along the path.
  • Optimality: Yes, if step cost = 1.
  • Time Complexity: O(bdb^d))
  • Space Complexity: O(bd)
Completeness Optimality Time Complexity Space Complexity
DFS Yes No O (bmb^m) O (bm)
BFS Yes Only when cost =1 O (bdb^d) O (bdb^d)
UCS Yes Yes O (b1+⌊C∗+ϵ⌋b^{1+\lfloor C^*+\epsilon \rfloor}) O (b1+⌊C∗+ϵ⌋b^{1+\lfloor C^*+\epsilon \rfloor})
DLS No No O (bl(b^l) O (bl(bl)
IDS Yes Only when cost =1 O (bdb^d)) O (bd)
ILS Yes Yes O (b1+⌊C∗+ϵ⌋b^{1+\lfloor C^*+\epsilon \rfloor}) O (b(1+⌊C∗+ϵ⌋)b(1+\lfloor C^*+\epsilon \rfloor))

Informed Search Strategies（启发式搜索）

启发式搜索的目的是通过引入Heuristics 针对 Forward Cost 进行估计，提高搜索效率

Heuristics

启发式函数，(Heuristics)，是针对当前状态 n 到 Goal State 之间最短路径的估计，一般用 h (n) 表示。H (n) 一般满足以下性质：

  • h (n) ≥ 0 for all states;
  • h (n) = 0，则 n 到达了终点；
  • h (n) = ∞，则 n 则无法到达终点；
    一般则设计 h (n) 时，需要考虑 h (n) 的计算效率等因素。

Greedy Searchl (贪心法)

对于当前的需要考虑的 Successors，通过 f (n) = h (n) 排序，选取最小的 f (n) 对应的状态（与终点最近的状态）进行 Expand。

本质上是UCS 和GBFS 的结合，采用Priority Queue 维护Partial Solution；Priority Queue 中的元素优先级由f(n) = g(n)+h(n) 决定，其中g(n)的定义与UCS 中一致；h(n) 则是启发式函数；出队入队过程与上文中的Uninformed Search 完全一致。

Admissible:if0⩽h(n)⩽h∗(n)0\leqslant h(n)\leqslant h^*(n)​,then h(n) is admissible.

这里可以看到，h(n) 对于我们的算法而言，希望能够更好地接近h∗(n) 真值。当我们越接近时，就能够更高效地找到最优解。

只有当h(n)是admissible的，A*算法才是最优的。

code display：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
def aStarSearch(problem, heuristic=manhattanHeuristic):
    """Search the node that has the lowest combined cost and heuristic first."""
    "*** YOUR CODE HERE ***"
    path = util.Path([problem.getStartState()], [], 0)
    priority=path.cost+heuristic(path.locations[-1],problem)
    if problem.isGoalState(problem.getStartState()):
        return []

    fringe = util.PriorityQueue()
    fringe.push(path,priority)

    while not fringe.isEmpty():
        current_path = fringe.pop()
        current_loc = current_path.locations[-1]
        if problem.isGoalState(current_loc):
            return current_path.actions
        else:
            successors = problem.getSuccessors(current_loc)
            if bool(successors):
                for successor in successors:
                    next_loc = successor[0]
                    next_action = successor[1]
                    next_cost = successor[2]
                    if next_loc not in current_path.locations:
                        locations = current_path.locations[:]
                        locations.append(next_loc)
                        all_actions = current_path.actions[:]
                        all_actions.append(next_action)
                        next_cost = current_path.cost + next_cost
                        path = util.Path(locations, all_actions, next_cost)
                        priority=path.cost+heuristic(path.locations[-1],problem)
                        fringe.push(path,priority)

    return []